Warning: This issue contains graphs, statistics, and a cameo from kurtosis. Side effects may include flashbacks to math class trauma and an urge to throw your phone. Reader discretion is advised.
It doesn’t matter how often you win if every once in a while you risk losing everything you’ve made and more. That’s what skewness captures, and with it, the reality of asymmetric payoffs.
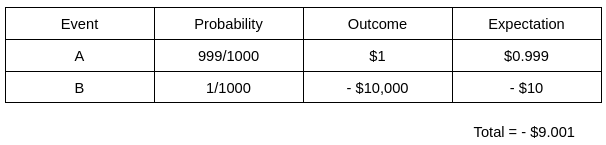
Take this game: you have 999 chances in 1,000 of winning $1, and 1 chance in 1,000 of losing $10,000. On the surface, it looks safe: a 99.9% chance of winning! But in reality, it’s a terrible bet. Why? Because the expected value (probability times the magnitude of the outcomes) is negative. The expectation from such a bet is a loss of close to $9. Maximizing the probability of winning does not necessarily lead to maximizing the expectation from the game when one’s strategy involves skewness, i.e., a small chance of a large loss and a large chance of a small win. You’re trading small, frequent wins for the risk of rare but catastrophic losses.
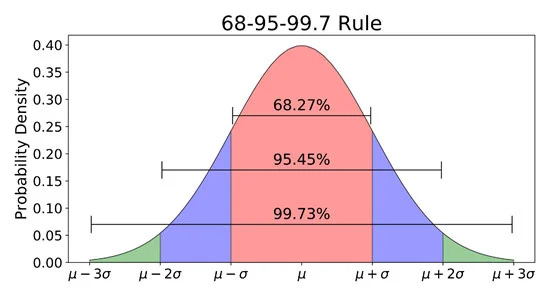
Asymmetry means the left side of a curve does not mirror the right side. In statistics, this imbalance is measured as skewness. In a perfectly symmetric curve, the mean, median, and mode all coincide. This represents the normal distribution, also known as the bell curve or Gaussian curve. The normal distribution appears frequently in daily life situations, such as the height, weight, IQ, or blood pressure of a population; however, many real-world phenomena do not follow it. That is when skewness becomes important. Distributions can be positively skewed (to the right) or negatively skewed (to the left). Note: The skewness of a normal distribution is zero.
Before I dive deeper, here’s a refresher:
Mean: the arithmetic average. Add all values and divide by the number of values.
Median: the middle value when data are ordered.
Mode: the value(s) that occur most frequently in the data.
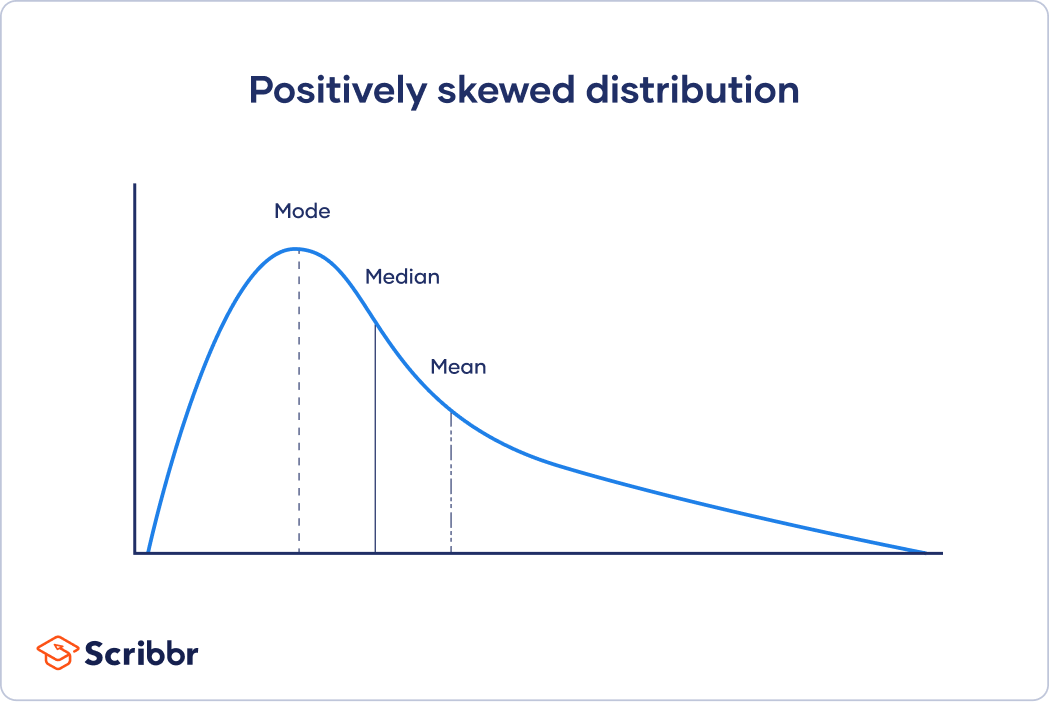
Positively Skewed Distribution
In a positively skewed distribution, most observations cluster on the left side, while the long tail extends to the right. This means: mean > median > mode.
Positive skewness can be illustrated with the following example.
You pay a premium on your insurance month after month, losing money, even though you are in good health. One day, you fall from your bicycle and break a leg. The insurance company pays the fat hospital bill. You lose small often, but gain big occasionally. That is positive asymmetry.
Other areas of life that are positively skewed with asymmetric payoffs include entrepreneurship, arts, venture capitalism, etc. You take multiple bets and lose most. However, periodically, a “dark horse” success will make up for all of the losses made. The challenging task is to persist until you have a breakthrough. Most people, if not all, are not wired to see their portfolios in red every morning they wake up. It takes an exceptional sort of psychological resilience to withstand the pain of frequent small losses for a huge payoff.
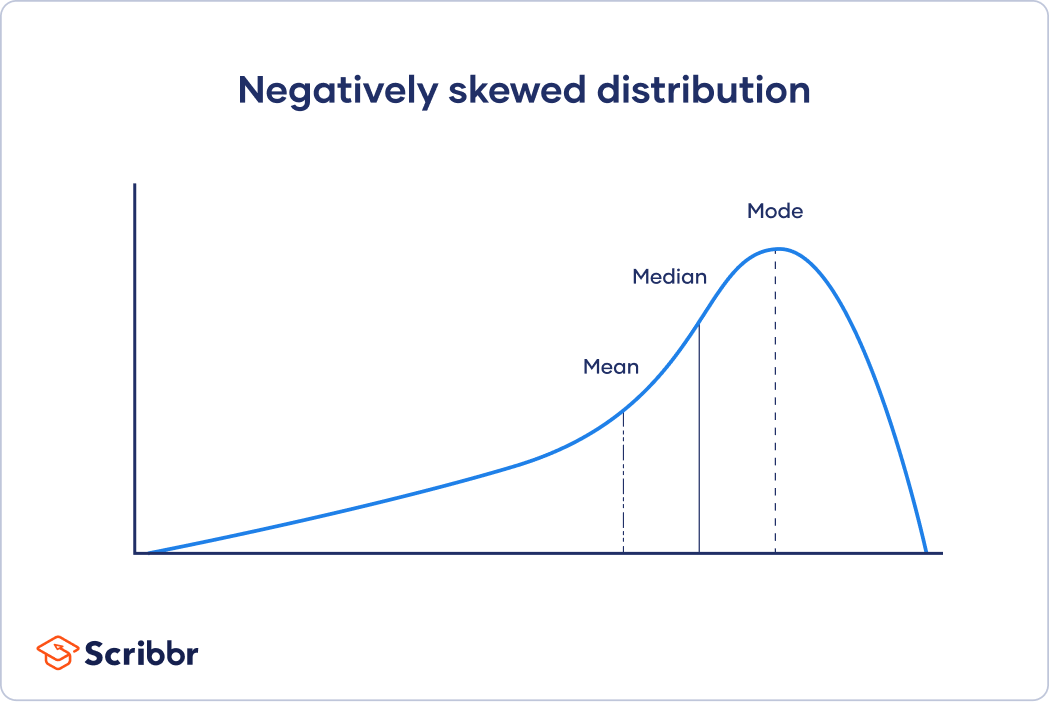
Negatively Skewed Distribution
In a negatively skewed distribution, most observations are on the right side, while the long tail extends to the left. This means: mean < median < mode. A negatively skewed distribution can be illustrated with the insurance example from earlier.
Consider yourself the founder of that same insurance company. People pay you a premium to insure their houses against natural disasters. Year after year, you collect small premiums from your customers. Then one day, a flood ravages the entire neighborhood. You pay your customers millions in damages against their insurance. You make money every month for years, and then suddenly lose everything you’ve made until that point due to one disaster. You enjoy a small upside, but suffer a large downside.
If you make $1 million for playing Russian roulette and continue to play, you are bound to find yourself in an obituary. Negative skewness feels safe in the short run but guarantees ruin in the long run. In such circumstances, the focus should be survival. Many dangerous sports (free diving, motorcycle racing, bull-riding, base jumping, etc) fall into this category: short bursts of pleasure against the risk of catastrophic loss. If there is a risk of ruin, you are better off avoiding it.
How do companies leverage this idea? Read my piece below to learn more.
The natural extension of skewness is to discuss the fat-tailed distributions. A normal distribution asymptotically approaches zero at a normal pace. In fat-tailed distributions, the tails asymptotically approach zero relatively faster or slower than a normal distribution. The values are higher as you move further out compared to a normal distribution. In other words, extreme values remain more likely than the bell curve would suggest (Black Swan, coming soon). Like skewness is a measure of asymmetry, there must be a way that captures how fast the tails approach zero. That method is called Kurtosis.
And before you throw your device against the wall in frustration, I’ll stop here. More on kurtosis later, folks.